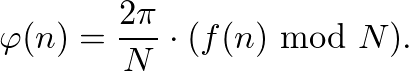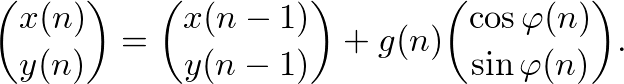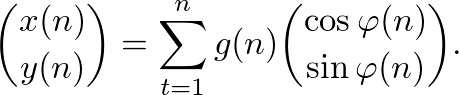Functional Walk Generator
A Walk is defined as a sequence of steps of connected graph vertices and graph edges. Functional Walks are generated by using a given function f(n) and an additional function g(n): (1) We start at some point w(n). (2) We divide 360 degrees in N equal directions. (3) We choose the direction for the next step by calculating f(n) mod N. (4) We move g(n) units in this direction and repeat the process. This public web application visualizes such walks in a great way and provides a variety of features to make further investigations on specific walks and walk theory in general convenient and interesting! More Information: Mathematics of Functional Walk Theory
Equation Input and Settings
f(n) = mod g(n) = n <
Block Mode
Random Slideshow
Show Advanced Settings and More
Information on Walk Theory
Facebook
Twitter
🌐  fschneider.info
▲ ▼
✕
Advanced Settings

Generation Speed:

Background Color:

Line/Block Color:

Line Width:

Block Size:

Vertex/Node Size:

Vertex/Node Color:

Build-In Functions
Basics
+, -, *, /
Basic arithmetic operations.
a^b, a**b
a to the power of b.
sin(n), cos(n)
Sine and cosine.
log(n)
Logarithm with base e.
a mod b, a % b
a modulo b.
Constants
PI, pi
Mathematical constant pi.
E, e
Mathematical constant e.
GAMMA, gamma
Mathematical constant Gamma.
Advanced Functions
ABS(n)
The absolut value of n.
CEIL(n)
Ceil function.
FACT(n)
n!, n factorial.
FIBO(n), F(n)
The n-th Fibonacci Number.
FLOOR(n)
Floor function.
OEIS: Axxxxxx
Use OEIS sequence.
PRIME(n), P(N)
The n-th prime number.
PRIMEDELTA(n), PD(n)
The difference of the n-th prime numbers.
SEQ: a,b,c,d,...
Use personal number squence.
SIGMA(n)
Devisor fum function.
TAU(n)
Devisor counting function.
Mathematics of Functional Walk Theory
A Walk is defined as a sequence of steps of connected graph vertices and graph edges. Functional Walks are generated by using a main function f(n) and an additional step function g(n):

(1) We are at some point w(n) = (x(n),y(n)). For n = 0 we define w(0) = (0,0).
(2) We divide the 360 degrees or 2π in N equal directions.
(3) We calculate the direction for the next step by
(4) We move g(n) units in this direction and repeat the process.
This process can be summarized trough the recursion
The walk is generated by adding steps, which may be represented as vectors. The recursion yields for the position (x,y) at a given moment n
The hole walk is therefore given by W(f,g,N). Fascinating patterns emerge very quickly, e.g. by applying f(n) = n. But also a variety of challenges and research opportunities arises when explaining patterns, predicting walks, describing walks as curves or investigating further properties. Also note the build-in OEIS tool.

Further Links: Wolfram: Walk, Wikipedia: IFS, Walk Pattern Gallery
Dark Theme ON/OFF
💡